Tìm hiểu thuật ngữ Toán học số nguyên là gì, số thực là gì?

1. Tổng quan về số nguyên

1.1. Khái niệm số nguyên là gì?

Số nguyên là một trong những thuật ngữ thường thấy trong Toán học. Để cụ thể hơn, tập hợp số nguyên bao gồm số nguyên dương, số nguyên âm và số 0.

Z là ký hiệu của tập hợp số nguyên, ký hiệu Z là viết tắt của chữ số trong tiếng Đức có tên là Zahl. Tập hợp số nguyên Z là tập hợp con của hai tập hợp lớn hơn đó là tập hợp số hữu tỉ Q và số thực R. 

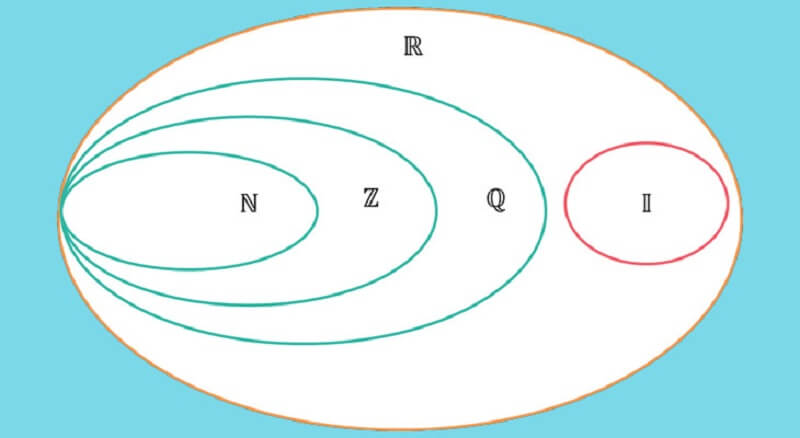
Đồng thời tập hợp số nguyên Z cũng là tập hợp mẹ của tập hợp số tự nhiên N, cùng các tính chất tương đồng như tập hợp số tự nhiên, tập hợp số Z là vô hạn nhưng đếm được. Do đó, tập hợp số nguyên Z có thể được chia thành 2 tập hợp con là Z- (số nguyên âm) và Z+ (số nguyên dương).

1.2. Thuộc tính của số nguyên trong Toán học

Theo nguyên tắc Toán học mà tập hợp số nguyên Z sẽ có những thuộc tính như sau:

- Thông thường sẽ không có khái niệm nhất định về số nguyên lớn nhất và số nguyên nhỏ nhất bởi khái niệm lớn nhất và nhỏ nhất sẽ dựa vào những điều kiện trong từng trường hợp.

- Số nguyên âm lớn nhất là -1 và số nguyên dương nhỏ nhất là -1.

- Số nguyên Z bao gồm vô số tập con hữu hạn và các tập con này sẽ có số nguyên nhỏ nhất, lớn nhất và không có một số nguyên nào nằm giữa hai số nguyên liên tiếp.

2. Tổng quan về số thực

2.1. Khái niệm số thực là gì?

Số thực (hay còn gọi là Real numbers), là tập hợp bao gồm các số dương (1, 2, 3), số 0, số âm (-1, -2, -3), các số hữu tỉ và các số vô tỉ.

Mọi người có thể hiểu đơn giản về số thực là tập hợp các số hữu tỉ và vô tỉ.

Cụ thể, tập hợp số thực sẽ được kí hiệu là R (trong đó: R = Q U I).

Tập hợp số thực sẽ bao gồm các số tự nhiên, số nguyên, số hữu tỉ và số vô tỉ, đây được coi là một hệ thống đại số đa dạng và là tập hợp số lớn nhất. Ngoài ra, ngoại trừ số 0 nằm ở vị trí trung tâm của trục số thì bất kỳ số thực nào đó cũng đều có thể là số dương hoặc số âm. 

Bản chất của tập hợp số nguyên R cũng tương đồng như các tập con khác bởi chúng đều là các tập hợp số vô hạn, tuy nhiên quy mô của tập hợp này quá đa dạng nên làm cho số lượng số thực trở nên nhiều vô kể.

Có lẽ bạn chưa biết, khái niệm số thực được sử dụng lần đầu tiên vào thế kỷ XVII, được sáng lập bởi nhà toán học người Pháp có tên là René Descartes với mong muốn thể hiện các giá trị nghiệm của đa thức và phân biệt với các nghiệm ảo. 

2.2. Nghiên cứu tính chất và thuộc tính của số thực

2.2.1. Tính chất

Mọi người cần lưu ý một số tính chất của số thực sau đây:

- Nếu một số thực bất kỳ nào đó khác 0 thì phần lớn sẽ là số âm hoặc số dương.

- Tổng hoặc tích của hai số thực (không âm) được gọi là số thực không âm.

- Số thực có hệ thống các tập hợp con vô hạn (có thể đếm được) và có khả năng thể hiện bằng biểu diễn thập phân.

- Ngoài ra, số thực còn có thể được sử dụng để thể hiện các phép đo đại lượng Toán học.

2.2.2. Thuộc tính

Một số thuộc tính của số thực cần ghi nhớ:

- Thuộc tính trường có thứ tự và chỉ ra rằng các số thực bao gồm một trường với phép nhân và phép cộng và cả phép chia cho các tập hợp số khác 0. Ngoài ra, chúng còn được điều chỉnh hoàn toàn trên trục hoành theo cách phù hợp nhất với phép nhân và phép cộng.

- Thuộc tính cận trên thấp và được thể hiện nếu tập hợp một số thực không trống có giới hạn trên và có cận trên thì đó chính là các số thực nhỏ nhất.

3. Phân biệt sự khác nhau giữa số nguyên và số thực

3.1. Số nguyên

Đối với số nguyên thì không có số nguyên nào là lớn nhất và cũng không có số nguyên nào nhỏ nhất. Đặc biệt là luôn có phần tử lớn nhất và phần tử nhỏ nhất trong một tập con hữu hạn bất kỳ của tập hợp số nguyên Z.    

3.2. Số thực

Bất kỳ số thực nào đó khác 0 đều thuộc số âm hoặc số dương, số thực có một hệ thống các tập con vô hạn đếm được của các số thực chẳng hạn như số hữu tỉ, số nguyên, đại số và số tính toán, … 

Mỗi tập hợp đều thuộc tập hợp con của tập hợp tiếp theo, tuy nhiên phần bù của tất cả các tập hợp này bao gồm số thực vô tỷ, số siêu việt, thậm chí cả số không thể tính được với các số thực đều thuộc tập hợp vô hạn không có khả năng đếm được.

Tổng và tích của hai số thực không âm đều là số thực dương, trường hợp này có thể tạo thành một vành số dương. Do đó tập hợp số nguyên có khả năng tạo nên một thứ tự tuyến tính của các số thực dọc theo một trục số nhất định.

Tập hợp các số thực tạo nên một tập hợp vô hạn cho dãy số mà không có sự tác động tới tập hợp vô hạn của dãy số tự nhiên trong toán học. Điều này tức là sẽ không thể đếm được các số thực, tuy nhiên các số tự nhiên được gọi là tập hợp vô hạn có khả năng đếm được.

4. Tổng hợp những tập hợp số cơ bản khác trong Toán học

4.1. Tập hợp số tự nhiên (ký hiệu: N)

Tập hợp số tự nhiên vốn là tập hợp số đầu tiên được hình thành trong lịch sử loài người đã lâu. N là ký hiệu của tập hợp các số tự nhiên và là tập hợp số cơ bản nhỏ nhất trong hệ thống các tập hợp số, chẳng hạn tập hợp số tự nhiên sẽ bao gồm 0, 1, 2, 3, …. Những con số này đã được phát hiện và sử dụng trong quá trình đếm, ghi chép và lưu trữ thông tin. 

4.2. Tập hợp số hữu tỉ (ký hiệu: Q)

Q là tập hợp của các số hữu tỉ, đây là những số có thể được biểu diễn ở dạng phân số với điều kiện cả hai số a và b đều là số nguyên và  phải khác 0. Tập hợp số hữu tỉ Q cũng giống như tập hợp số tự nhiên N hay tập hợp số nguyên Z, chúng đều là những tập hợp số vô hạn nhưng có thể đếm được. 

4.3. Tập hợp số vô tỉ (ký hiệu: I)

Tập hợp số vô tỉ I là những con số không thể biểu diễn dưới dạng phân số, do đó, những số vô tỉ thường được thể hiện một cách đơn giản là các số thực không phải số hữu tỉ.

4.4. Tập hợp số phức (ký hiệu: C)

Tập hợp các số phức C có dạng (a + bi) với a và b là hai số thực và i là đơn vị ảo, chính vì dạng biểu diễn này mà số phức sẽ chia làm hai phần là phần ảo và phần thực.

Trên đây là những thông tin chi tiết và cụ thể nhất về số nguyên là gì, số thực là gì cho bạn đọc tham khảo. Hy vọng sau khi đọc xong bài viết này bạn đọc có thể áp dụng kiến thức vào trong bài tập của mình, đừng quên theo dõi các bài viết mới nhất của chúng tôi qua trang web timviec365.vn để cập nhật nhiều kiến thức mới hàng ngày bạn nhé.